Why Are Computational Experiments Important?
 The ability to explain and predict is what makes science so important and useful. An observation that cannot be explained
is not understood. Only after a theory is developed to explain it can it be considered as part of science. Once a theory is established,
it can be used to reliably predict new things and guide further explorations. The development and application of theories used to rest
only on real experiments. With the advancement of computational science, accurately modeling natural phenomena has become a reality.
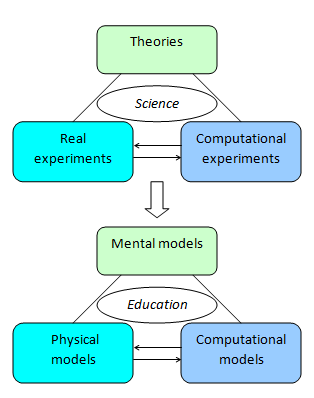
Science now increasingly relies on computational experiments—computer simulation of real experiments—to understand how the world works,
especially when the real experiments are too hard, too dangerous, or too expensive to carry out. Theories, experiments,
and computation are now considered the three pillars of science.
The ability to explain and predict is what makes science so important and useful. An observation that cannot be explained
is not understood. Only after a theory is developed to explain it can it be considered as part of science. Once a theory is established,
it can be used to reliably predict new things and guide further explorations. The development and application of theories used to rest
only on real experiments. With the advancement of computational science, accurately modeling natural phenomena has become a reality.
Science now increasingly relies on computational experiments—computer simulation of real experiments—to understand how the world works,
especially when the real experiments are too hard, too dangerous, or too expensive to carry out. Theories, experiments,
and computation are now considered the three pillars of science.
The picture of these three pillars of science maps to a similar picture of three pillars of science education. A primary goal of science education is to help students develop robust mental models of science concepts and apply them to solve problems. Laboratory activities provide a learning pathway to building mental models from doing real experiments. Computational experiments provides another pathway, which has many advantages such as low cost and safety compared with real experiments. However, they cannot replace hands-on laboratory experiences. How to integrate computational experiments into the curriculum to enhance learning is an interesting research topic.
On a separate note, computational experiments may provide an important tool for defining and understanding computational thinking in the context of science.
Why are process models important?
There are two types of computational models: data model and process model. Computational experiments mainly concern process models.
Data models are very common. For instance, geographic information system (GIS) software such as Google Earth are driven by a data model that is linked to location (x, y, z). These data are static—they were generated from land surveys and remain unchanged until the next update. Another example is the protein data bank that contains tens of thousands of structure data of macromolecules obtained from crystallography. The structure data are coordinates (x, y, z) that define the positions of atoms in macromolecules. These data are static, characterizing stable conformations of macromolecules.
Nature is not static, however. Our world is fundamentally dynamic. It is full of many different kinds of processes—creep, flow, growth, explosion, flying, and so on. We live in a four-dimensional world (x, y, z, t), not a three-dimensional one (x, y, z). Modeling the four-dimensional world is the domain of process models. Computational experiments investigate process models. Computational experiments can not only be used to reconstruct what has happened, but also be used to predict what will happen.
Computational experiments lend great power to science education, because they can show important processes to students and be manipulated to explore causality. If a picture is worth a thousand words, a dynamic computational experiment is worth many thousand pictures. The salient nature of a computational experiment could present a much better learning experience than didactic instructions with static illustrations. Unlike a movie or an animation, an interactive experiment is not premade or scripted—it is computed in real time and can respond to the user's interventions in many different ways. This is a significant advantage of a computational experiment over a movie or an animation. If you are watching a movie, you cannot change the plot. If you are interacting with an animation, you probably have a number of limited, exact outcomes depending on the combination of preset rules. But if you are conducting a computational experiment or designing a new one, no one can predict exactly what results you will find. Computational experiments can exhibit a similar degree of variety and diversity that we observe in real experiments.
To ensure the scientific accuracy, a computational experiment is based on fundamental laws, such as Newton's Laws for classic mechanics, the Schrödinger equation for quantum mechanics, the Navier-Stokes equation for fluid dynamics, the Maxwell equations for electromagnetism, and so on. As such, a computational experiment will not only deliver the most important insights of science, but also open up countless opportunities for students to explore. Now that ordinary computers are powerful enough to run intense calculations, science education has an unprecedented opportunity of revitalization. Next generation digital textbooks could integrate computational experiments. Wherever you see a static illustration in a textbook today, you would see a computational experiment in tomorrow's digital textbooks. Your digital textbooks could have powerful built-in computational labs.