|
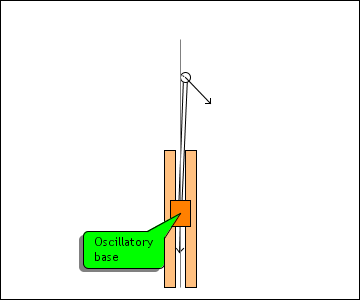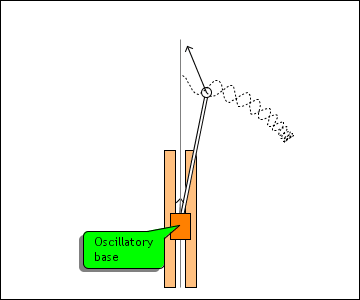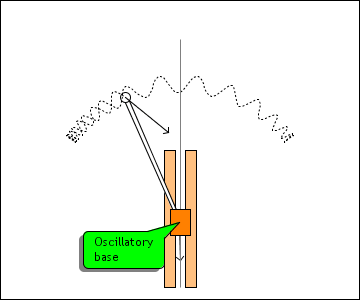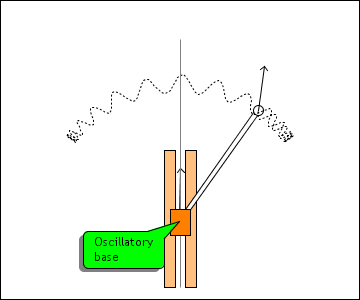
This simulation shows a strikingly counterintuitive result: an inverse pendulum can
be stablized by a rapidly oscillating base. If the perturbation is reasonable and the
oscillation is strong and frequent enough, the inverse pendulum can always recover
from the perturbation.
|
The above image is just an animated gif file. Click the above button, or
this link to launch the model.
|
|
System requirements:
You must have Java Version 5 or higher in order to run this program. Please
go to java.com to get the latest Java software,
if you are not sure.
|
|
Failed?
Check out the FAQ for troubleshooting.
|

